仕事とエネルギー | 初心者のための力学入門
今回は「仕事」「エネルギー」「仕事率」の言葉の意味を具体例も交えながらわかりやすく説明していきます。最後までお付き合いください。
力と運動方程式ががからない方は先にこちらもどうぞ。
力の分解がわからない方は先にこちらもどうぞ。
仕事
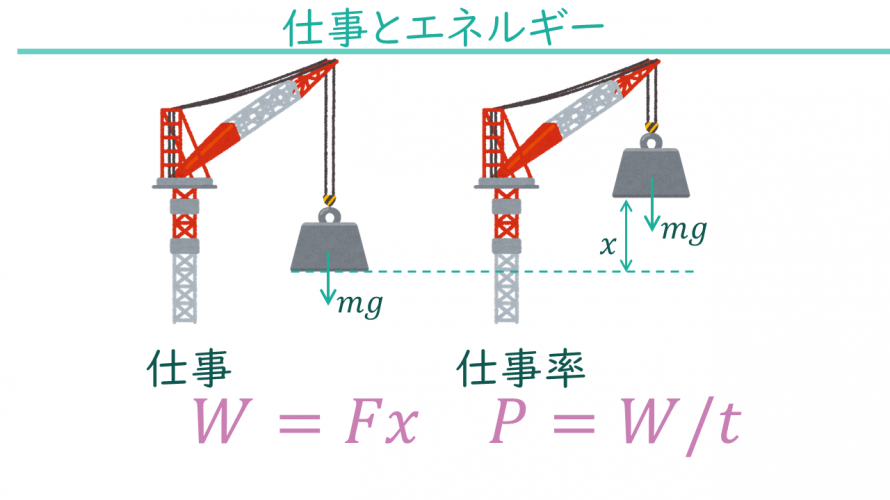
力学の世界における仕事とは力を加えて物体を動かすことです。
簡単な例で言うと、クレーンで物を持ち上げる動作などが仕事にあたります。仕事Wは加えた力Fと移動量xで表します。
$$W=Fx$$
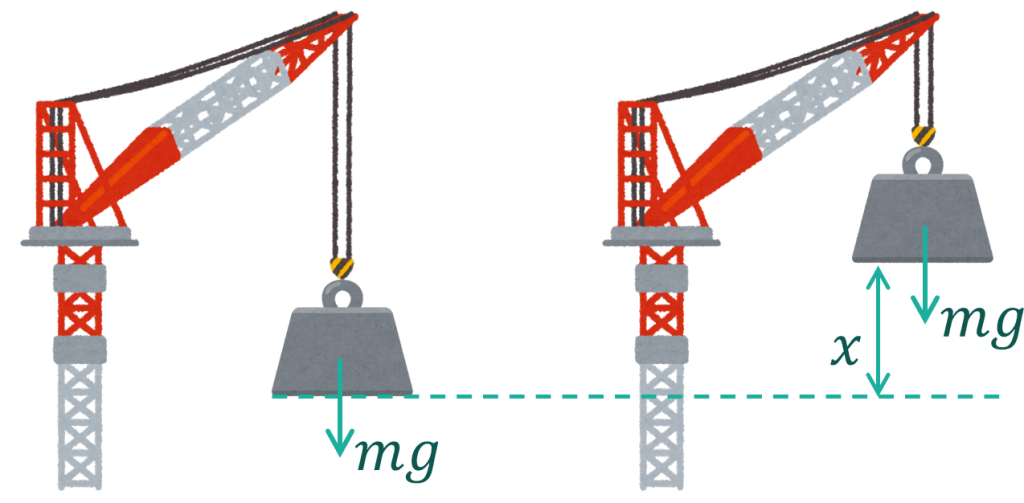
例えばクレーンで質量m[kg]の物体をx[m]持ち上げる場合は、
$$W=mgx$$
となります。
ここで注意したいのは、加えた力はすべて仕事に使われるとは限らないということです。
例えば次の図のように、斜め方向に力Fを加えて物体をx[m]引きずる場合、実際に仕事に使えているのは\(F\cos\theta\)だけで、\(F\sin\theta\)の方の力は仕事に寄与していません。
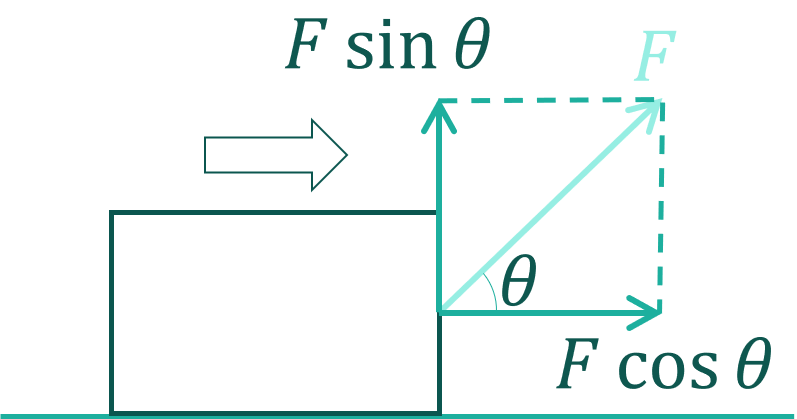
つまり、物体が動く方向と力の向きが異なる場合、力を分解して物体が動く方向の力だけを取り出す必要があります。この場合の仕事は次の式で得られます。
$$W=Fx\cos\theta$$
仕事Wの単位はJ(ジュール)です。式からも分かる通り、1Nの力で1m物体を動かしたときの仕事が1Jということになります。
エネルギー
エネルギーは仕事をする能力のことです。単位は仕事と同じJ(ジュール)です。
と言われてもよく分からないと思います。もう少しかみ砕いていうと、仕事というのは実際に何か物体が動いている時の話で、エネルギーというのは蓄えておくものの話です。
「エネルギーを使って仕事をする」「仕事によってエネルギーを蓄える」という言葉で仕事とエネルギーの関係を説明することができます。
具体例で言うと、「電池(エネルギー)を使ってモーターを回す(仕事)」や「風車を回して(仕事)発電をする(エネルギー)」などが挙げあれます。
このようにエネルギーと仕事は互いに交換されます。そのため単位は共通となっています。
エネルギーにはたくさんの種類があります。力学分野で言うと位置エネルギー、運動エネルギー、弾性エネルギーなどがあり、その他分野では電気エネルギー、磁気エネルギー、音エネルギーなどがあります。
仕事率
唐突ですが、階段を上るのも仕事と言えます。自分の体重を高いところまで持ち上げいます。
例えば1階から3階まで移動するとき、ゆっくり上るのと駆け足で上るのとでは疲労感が大きく異なると思います。
これが意味するのは、同じ仕事であってもどれだけの時間で行うかで負担が変わるということです。
そこで、この”負担”を表すために1秒当たりに行う仕事を仕事率\(P\)と呼ぶことにします。 仕事率\(P\) は仕事\(W\)と時間\(t\)を使って次の式で表します。
$$P=\frac{W}{t}$$
仕事率\(P\) の単位はW(ワット)です。電化製品の消費電力でお馴染みのあのワットと同じです。消費電力というのは、1秒間にどれだけの電気エネルギーを製品に供給するかを表しているので、まさに仕事率そのものです。
紛らわしいのですが、仕事を表す文字W(Workの頭文字)と仕事率の単位W(ワット)が同じになっています。しかし、当然これらは全くの別物です。
「仕事」と「仕事率」の言葉が似ていてすでに紛らわしいのに、文字も紛らわしくなっていて非常に厄介ですが、しっかり整理して覚えましょう。
「Work=仕事」というのは英語を学んでよく知っていると思うので、ここを基準に覚えるのが良いと思います。
ここまで説明してきた言葉をまとめると次の表のようになります。
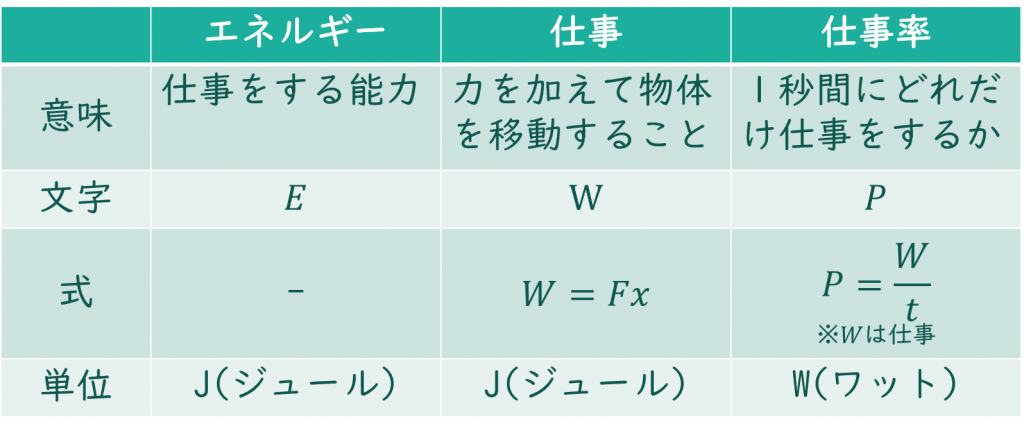
まとめ
仕事、エネルギー、仕事率について説明しました。
力学分野ではエネルギーと仕事が頻繁に登場し、電気分野では仕事率が頻繁に登場するので、結局全部重要です。それぞれの意味と式、単位をしっかり覚えておきましょう。
-
前の記事
力のモーメント | 初心者のための力学入門 2021.06.07
-
次の記事
記事がありません