摩擦力 | 初心者のための力学入門
摩擦力は接触する二物体が滑り合う時に働く力です。日常生活でもよく出てくる現象なので皆さんよく知ってると思います。
今回はこの摩擦について力学的な説明をします。運動方程式を理解していることが前提となるので、わからない方は先に学習してください。
摩擦力
まずは復習から
今回は水平な面の上で物体を滑らせるケースを考えてみます。とりあえず、面の上に物体を置いてみます。物体の質量はm、重力加速度はgとします。
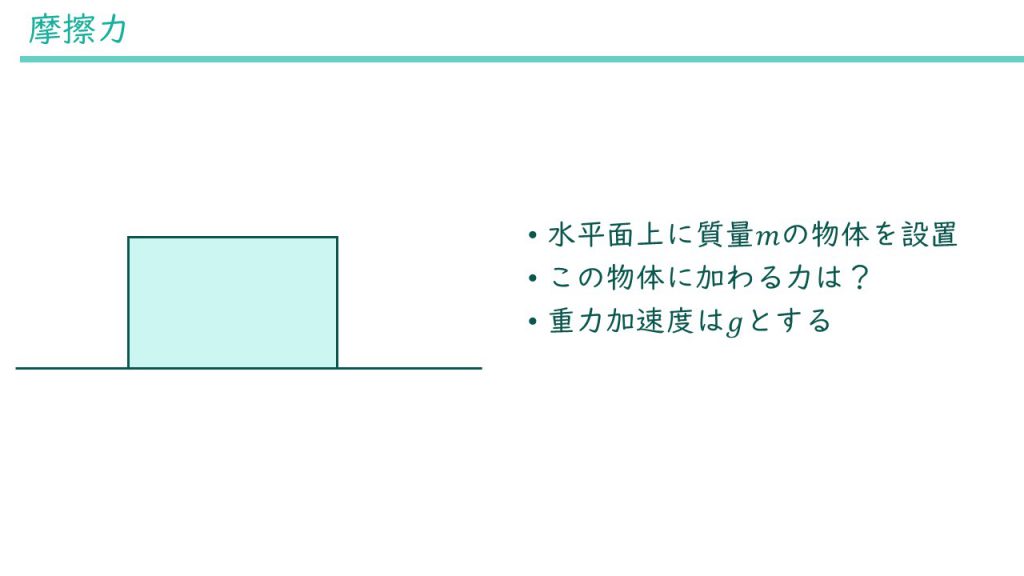
この時に物体に加わる力を考えてみてください。前回の復習です。答えが予想できたら先に進んでください。
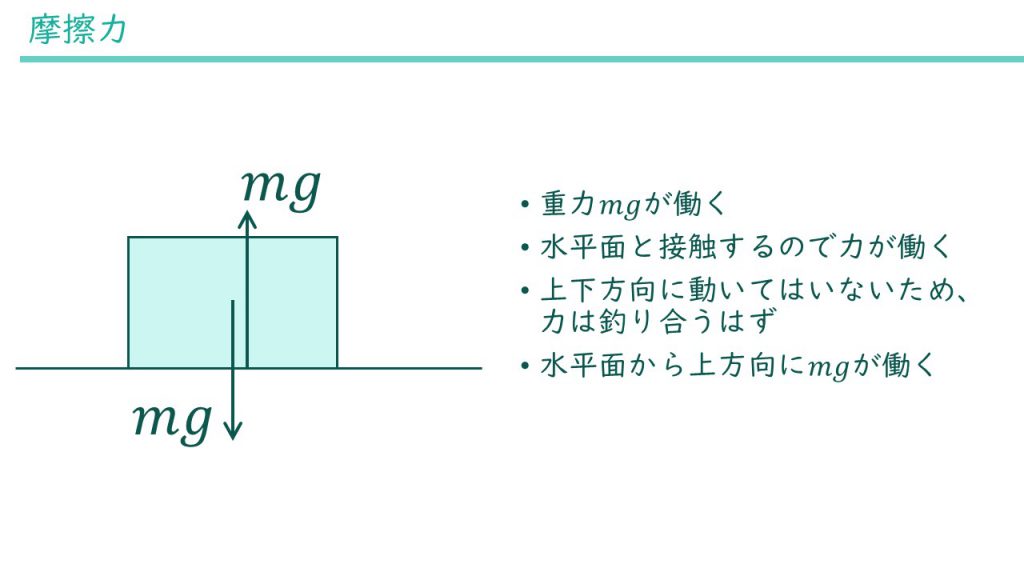
答えは下図のようになります。物体には重力mgが加わり、重力と釣り合うように水平な面から力mgが加わっています。
摩擦力が働く位置と向き
物体を滑らせたいので、横から力を加えてみましょう。横からの力をFとします。物体は加速度aで左に移動します。
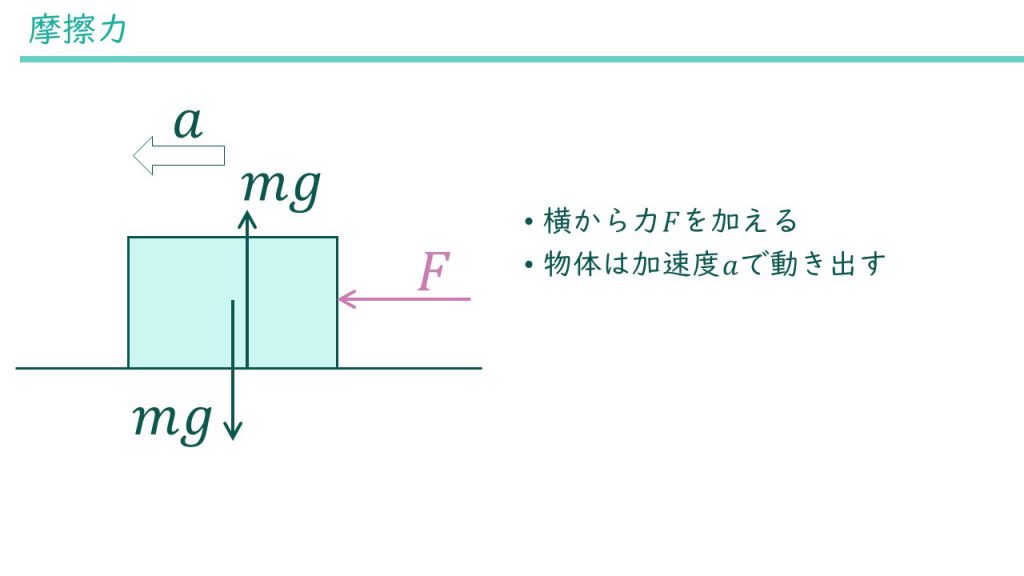
物体が左に動くときに摩擦が発生します。摩擦力働く位置と向きは先に答えを書いてしまいます。
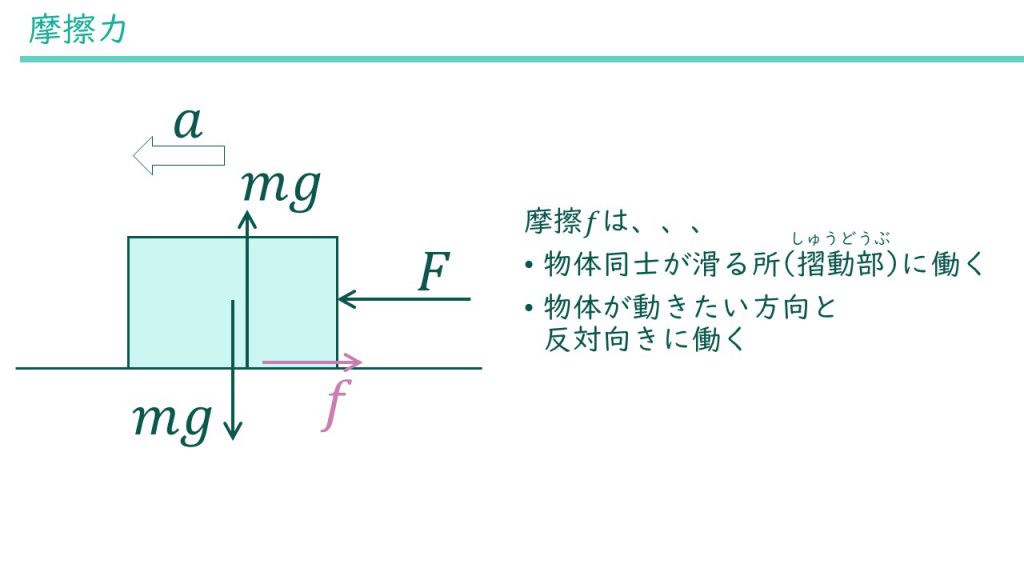
摩擦の特徴は次の2つです。
・2つの物体が滑る所(摺動部:しゅうどうぶ)に働く
・物体が動きたい方向と反対向きに働く
今回は水平な面と物体が滑り合っているのでこの面に摩擦力が働きます。右から力を受けて左に動こうとしているので、その反対の右方向に摩擦力がかかります。いったん摩擦力を\(f\)とします。
なぜ摩擦力の向きが反対になるのか、もう少し詳しく見ていきましょう。水平面と物体が接触している部分を、顕微鏡レベルで拡大してみるとこのようになっています。
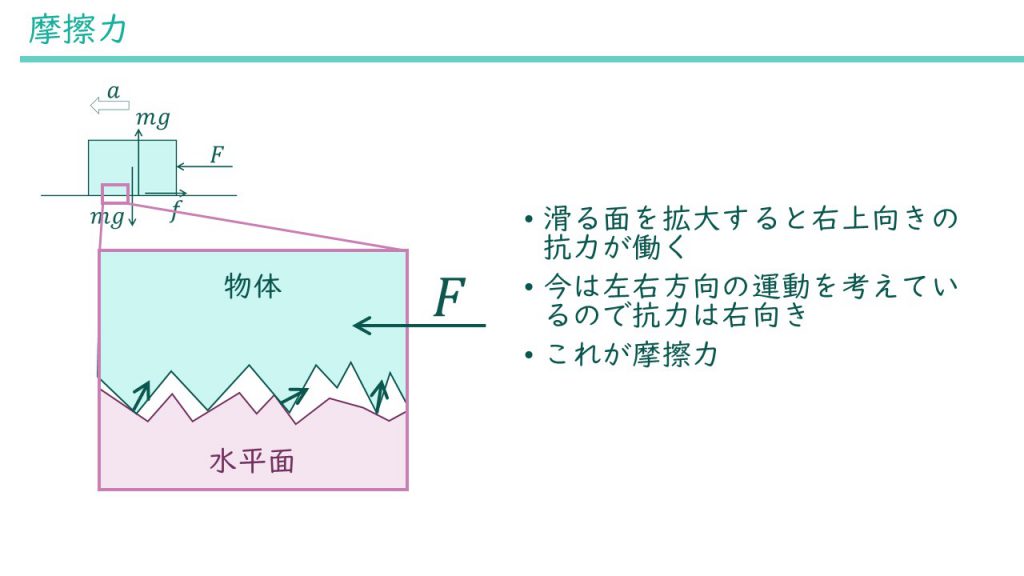
どんな物体も表面には細かい凹凸があります。物体同士が接触するとき、この凹凸が引っかかっています。この状態で上側の物体に右から力をかけると、引っかかっている部分に抗力(動きを妨げる力)が働きます。効力は右上向きになっていますが、左右方向の運動にのみ着目しているので抗力は右向きと考えます。この抗力こそが摩擦力です。
このイメージを持てれば摩擦の力の向きがわかると思います。
本当は表面の凹凸の引っ掛かり以外にも多くの要因が影響して摩擦力が決まります。しかし、今は摩擦力の向きを理解したいだけなのでこの程度の認識で十分です。
摩擦力の大きさ
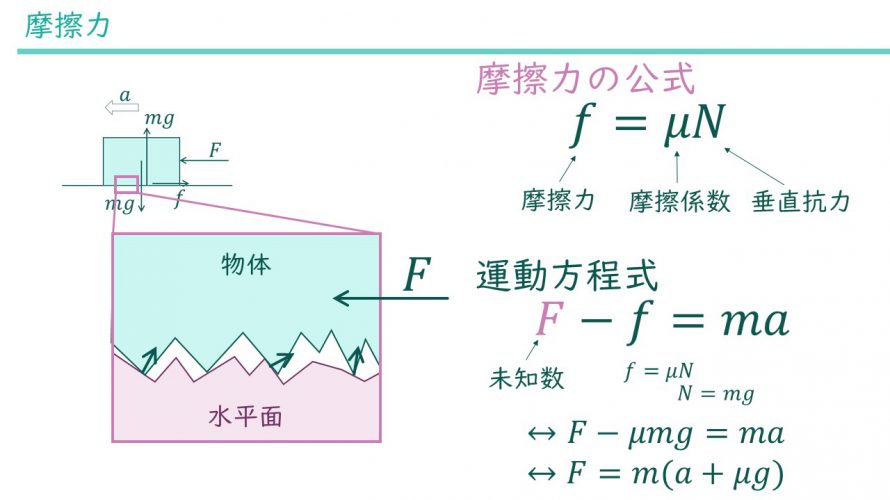
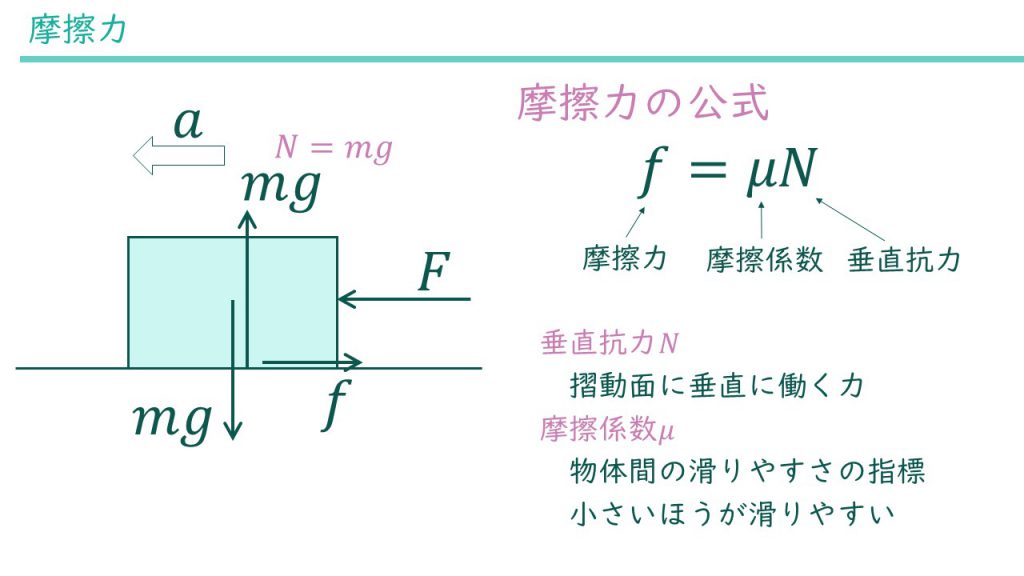
摩擦力の向きと位置はわかりました。あとは大きさが知りたいです。これが今回一番のポイントです。キーワードは「垂直抗力N」と「摩擦係数μ」です。摩擦力の大きさは摩擦係数×垂直抗力です。式で表すと次のようになります。
$$f=\mu N$$
垂直抗力は摩擦が発生している面に掛かっている力で、特に面に対して垂直な方向に働く成分のことです。「垂直な方向に働く成分」というのがピンとこないかもしれません。今回のケースでは摩擦面は水平方向に広がっています。水平に対して垂直な方向は鉛直方向です。鉛直方向とは重力が働く方向のことで、感覚的に言うと上下方向のことです。
くどくなってしまいましたが、まとめると、今回のケースでは「摩擦面に鉛直方向へ働く力」が垂直抗力になります。そしてそれは上方向を向いている\(mg\)のことです。
2つ目のキーワードは摩擦係数でした。摩擦係数は物体間の滑りやすさを表す指標で、小さければ滑りやすいことを、大きければ滑りにくいことを表します。私達がいま考えているレベルの力学では0~1の値を取ります。記号はμ(ミュー)を使います。
摩擦係数は先程説明した凹凸の具合や、形状、材質、潤滑剤の有無など様々な要因の影響を受けるので推測が難しいです。このため、摩擦係数は実験で求めるのが一般的です。
さて、物体に働く力の説明はすべて終わったので、図にまとめてみましょう。
試しに力\(F\)が未知数であると考えて、Fを求める式を立ててみましょう。
摩擦を含む運動方程式
運動を考える上では、直行する2つの方向の運動は分けて考えます。今回の例でも上下左右の全方向に力が働いていますが、上下方向と左右方向に分けて考えることができます。
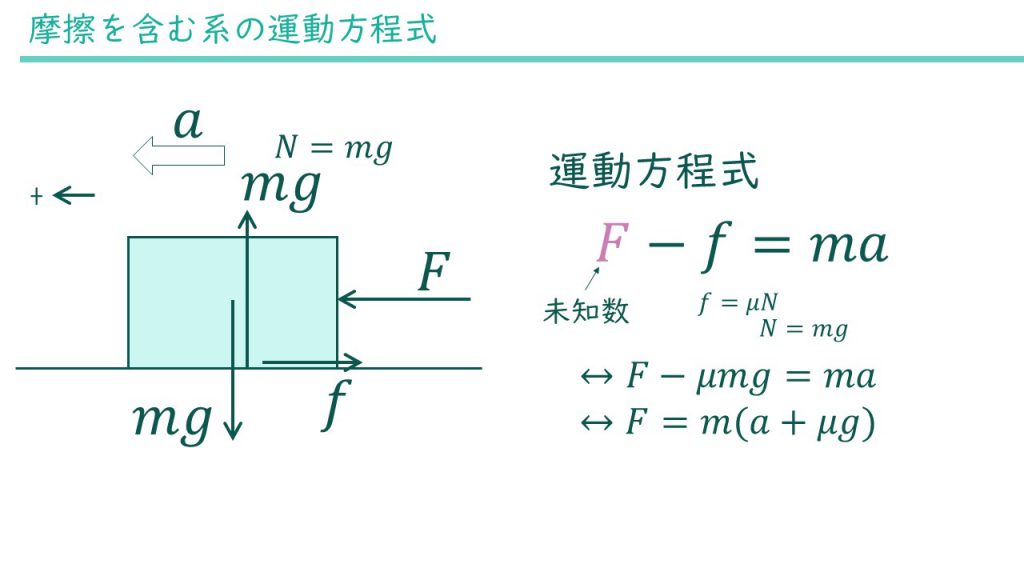
力Fを求めたいので、左右方向の運動方程式を立てます。左方向を正とします。
$$F-f=ma$$
\(f=\mu N\)と\(N=mg\)が成り立つので
$$F-\mu mg=ma$$
となります。あとはこの式をFについて解けば終わりです。
$$F=m(a+\mu g)$$
この式が何に役立つかというと、例えば富士急のドドンパのスタート時にどれだけの力が必要かを計算できたりします。実際に計算してみましょう。
余談ですが、そもそもドドンパはド・ドドンパにリニューアルされているんですね。知らなかったです。ド・ドドンパは8人乗りなので、一人60kgと想定すると人の質量は\(8\times60=480kg\)となります。車両重量はWikipediaによると4000kgだそうです。よって質量は合わせて4480kgとなります。
加速度は3.75Gです。Gは大文字ですが重力加速度のことです。つまり約9.81\(\mathrm{m/s^2}\)です。よって加速度は(3.75\times9.81=36.8\mathrm{m/s^2})程度です。
摩擦係数は完全に推測ですが、ジェットコースターに乗っていて摩擦による減速は感じたことがないので、相当低い値になっていると思います。仮に0.005としましょう。
これで必要な値はすべて揃いました。元の式に代入して計算すると、
$$F=4480(36.8+0.005\times9.81) ≒ 165000\mathrm{N}$$
と求まります。これは17000kgのものを持ち上げられるくらいの力です。計算が正しいか自信がなくなるくらい桁外れに大きい力ですね。。。
実際には乗員が8人とは限りませんし、天候によって摩擦係数も変わりますし、風の抵抗も受けたりしますし、考慮すべきことはもっとたくさんあります。開発者はあらゆる条件を考慮して問題が起きないように最適な力を設計します。設計により必要な力がわかると、それだけの力を出力できる動力原を選定します。ド・ドドンパはエアシリンダーを使っているそうです。
逆に使用できる動力が決まっていて、車両の重量と乗員数を調整することで加速度をコントロールする場合もあると思います。この場合は質量\(m\)を未知数と考えて方程式を解くことになります。
このように、運動方程式を立てるところまでは基本的に一本道で、状況に応じてどの文字について解くかが変わります。
静止摩擦力と動摩擦力
さて、これまで「摩擦力」という言葉を多用してきましたが、摩擦力には2種類あります。それが静止摩擦力と動摩擦力です。それぞれについて詳細に説明します。
動摩擦力
上で説明してきたものが動摩擦です。文字通り、物体が動いているときに働く摩擦力です。動摩擦時の摩擦係数を特に動摩擦係数\(\mu’\)と言います。これまで説明の都合で摩擦係数\(\mu\)と書いていましたが、後述する静止摩擦係数\(\mu\)と区別するために、動摩擦係数は\(\mu’\)を使用するのが一般的です。
動摩擦は常に\(f=\mu’ N\)の公式に従います。つまり、横から受ける外力\(F\)や物体が動く速度の影響は受けないということです。
静止摩擦力
一方静止摩擦力は、物体が動いていないときに働く摩擦力です。静止摩擦力は物体に働く力によって大きさが変わります。具体例を見ながら考えていきましょう。
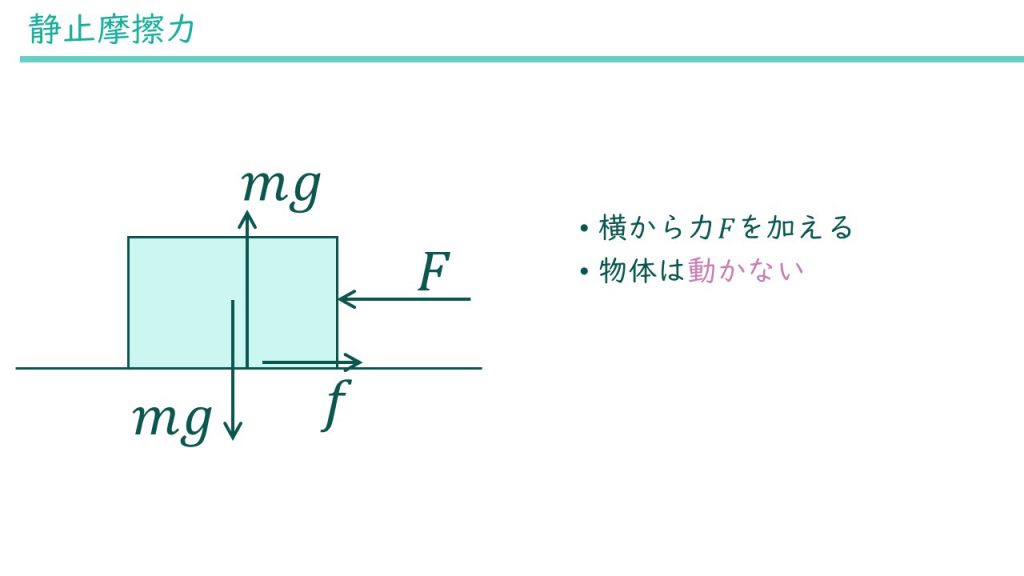
上で説明した例とよく似ていますが、加速度\(a\)がないという違いがあります。つまり、物体は動いていないということです。横から力を受けているのに動いてはいないのです。
重いものを引きずろうとして力を加えても全然動かないことがありますよね。あの感覚です。実際は重いものに限らずどんなものでも、動き出すためにはある程度の大きさの力が必要で、それ以下の力では物体は動きません。
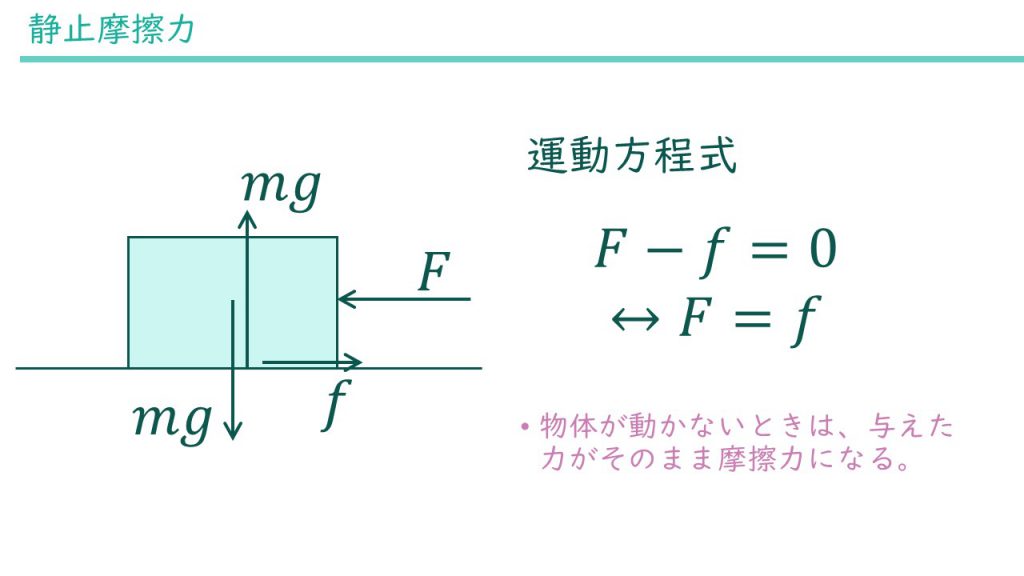
さて、左右方向の運動方程式を立てると
$$F-f=0\\\leftrightarrow F=f$$
となります。物体が動いていないため右辺は0になっています。その結果、加えた力と摩擦力が釣り合うという示すシンプルな式となります。
つまり、物体が動き出すまでは、加えた力(の摺動面と平行な成分)がそのまま摩擦力になるということです。
そして、物体が動き出すギリギリの静止摩擦力を最大静止摩擦力と言い、その摩擦係数を静止摩擦係数と言います。静止摩擦をはこのギリギリの時だけ\(f=\mu N\)の公式が成り立ちます。
静止摩擦と動摩擦の比較
ここまでの説明をまとめると次のようになります。
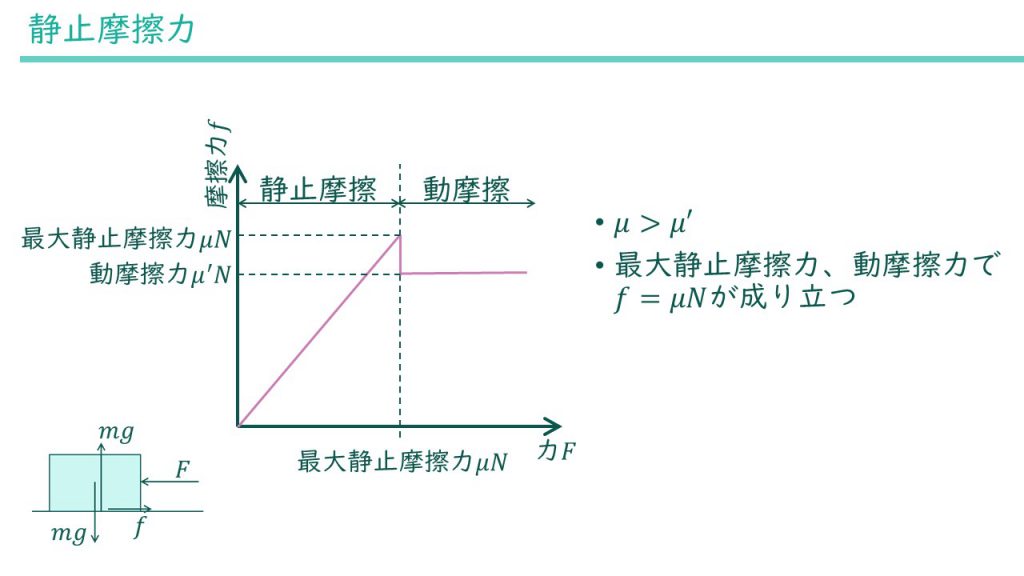
物体に徐々に外力を加えていくと、最初のうちは加えた外力がそのまま摩擦力になります。外力が\(f=\mu N\)を満たす最大静止摩擦力になると、物体が動き出し、静止摩擦から動摩擦に変化します。動摩擦になった以降は常に一定の摩擦力\(f=\mu’ N\)となります。
静止摩擦係数\(\mu\)と動摩擦係数\(\mu’\)を分けて考えていたのは、それぞれ値が異なるからです。値を比較すると\(\mu>\mu’\)となります。つまり最大静止摩擦力のほうが動摩擦力よりも大きいと言うことです。
グラフを見ると静止摩擦から動摩擦に移るときに摩擦力がガクッと落ちています。摩擦係数の差によってこのような現象が起きています。日常生活でも物を動かすときには動き出しが一番重く感じて、動き出すと少し軽くなる現象は経験したことがあるのではないでしょうか?
まとめ
摩擦力がかかる場所、向き、大きさを求める方法と、摩擦を含む系の運動方程式の立て方を説明しました。摩擦は力学を勉強するうえでも、機械を設計するうえでも確実に理解しておく必要があります。理解できるまで繰り返し読んで確実に身に着けるようにしましょう。
-
前の記事

運動方程式 | 初心者のための力学入門 2021.05.14
-
次の記事
摩擦係数の測り方|初心者のための力学入門 2021.05.31
