力のモーメント | 初心者のための力学入門
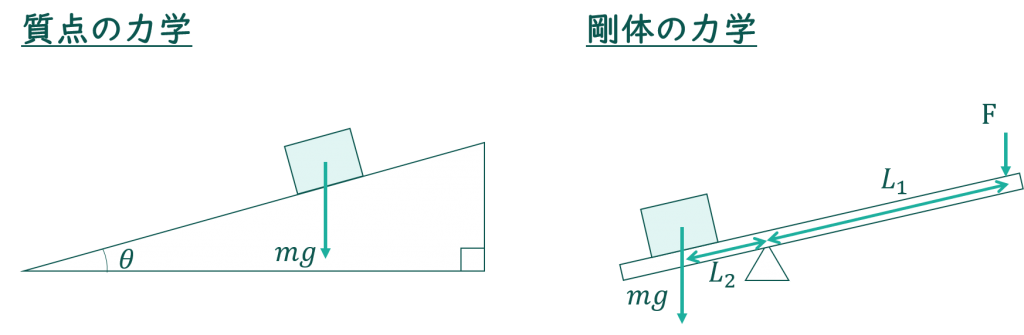
今回は力のモーメントの説明をします。これまでに運動方程式から摩擦力まで説明してきましたが、これらの運動では物体の大きさが無視できました。極端に言えば、自動車のような大きい物体でも、大きさが無い「点」でも同じ計算になります。この特徴から大きさが無視できる力学は質点の力学というジャンルに分けられます。
力のモーメントは質点の力学とは反対に、物体の大きさが重要です。このような力学は剛体の力学というジャンルに分けられます。それでは始めましょう。
力のモーメント
てこの原理
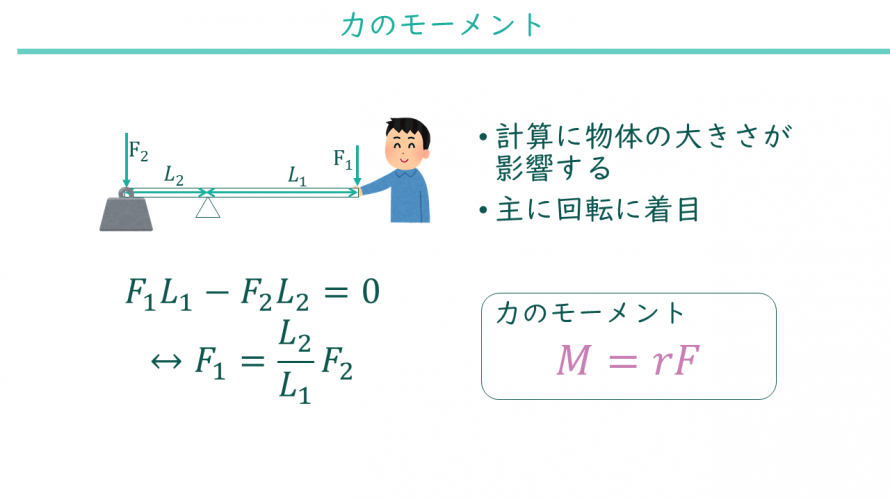
力のモーメントは簡単に言うとテコの原理の拡張です。
小学校でテコの原理は次のように習ったと思います。

- 支点、力点、作用点がある
- 支点と力点が遠いほど軽い力で持ち上げられる
- 支点と作用点が近いほど軽い力で持ち上げられる
これを数式で表し、力点が複数ある場合などにも対応したものが力のモーメントです。
一番シンプルなモーメント
まずは最もシンプルな例としてドアノブの構成で考えてみます。棒の左端に支点\(O\)があり、右端に力\(F\)が働いています。支点\(O\)から力\(F\)までの距離は\(L\)とします。
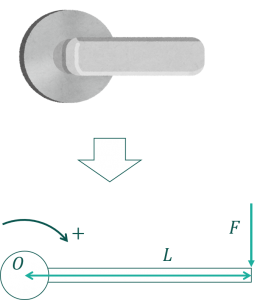
早速モーメントを求めてみましょう。モーメント\(M\)は腕の長さ\(r\)×力\(F\)で表します。式で言うと、
$$M=rF$$
となります。また、時計回りに加わるモーメントを正、半時計回りに加わるモーメントを負で表します。今回は棒を時計回りに回転させるような力が働いているのでモーメントは正の値になります。
腕の長さ\(r\)というのは支点から力までの距離のことで、今回は\(L\)にあたります。したがってモーメント\(M\)は次式で表せます。
$$M=LF$$
考察のために両辺を\(L\)で割ってみます。
$$F=\frac{M}{L}$$
モーメント\(M\)を定数だと仮定すると、この式は反比例の式になっていします。
つまり、同じモーメントを得たい場合、\(L\)が半分になると\(F\)が2倍になると言うことです。
ドアノブを使えば簡単に実験ができるので、ぜひ試してみてください。支点から遠いところに力を加える場合と、近いところに力を加える場合で必要な力が大きく変わることがわかると思います。
腕の長さの深掘り
モーメントを求める時に注意したいのは、腕の長さは回転中心(支点)から力点・作用点までの長さではなく、回転中心から力点・作用点に加わる力(ベクトル)までの距離だということです。言葉だとわかりにくいので次の例で考えてみます。
先程の例から棒を角度\(\theta\)だけ傾けています。力は変わらず鉛直方向(重力が働く向き。基本的に上下方向)下向きに働いています。
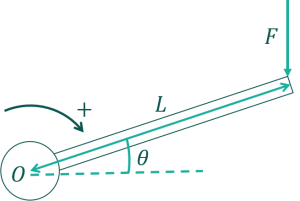
この場合腕の長さ\(r\)は、どうなると思いますか?
答えは次のようになります。
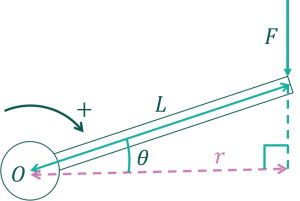
一般的に「距離」というのは2つのものを最短で繋いだときの長さを表します。点と直線の場合、点から直線に向かって垂直に引いた線(垂線)の長さが距離になります。力のモーメントも同様に、点から力に向かって引いた垂線が腕の長さになります。
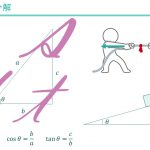
\(r\)の長さを求めましょう。垂線を引いたことによって直角三角形が形成されています。「直角三角形」「角度\(\theta\)」と言えば三角比です。
三角比がわからない方はこちらをどうぞ
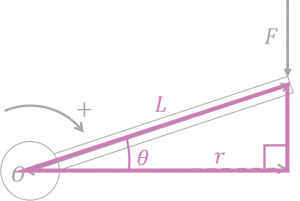
腕の長さ\(r\)を棒の長さ\(L\)と角度\(\theta\)を用いて表します。cosの定義を使用して
$$\cos\theta =\frac{r}{L}\\ \leftrightarrow r=L\cos\theta$$
となります。これが今回の例における腕の長さになっています。この式を\(M=rF\)に代入するとモーメントが次式で表されます 。
$$M=rF\cos\theta$$
半径方向の力
もっと極端な例を考えてみましょう。さらに角度を立てて、\(\theta=90^{\circ}\)の場合を考えてみましょう。図にすると次のようになります。
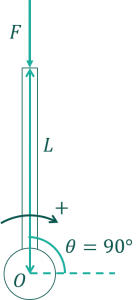
この時腕の長さはどうなるでしょうか?
前項で\(r=L\cos\theta\)という式を導出したので、この式に \(\theta=90^{\circ}\) を代入してみます。
$$r=L\cos\theta \\r=L\cos 90^{\circ} \\r=L\times 0\\ r=0$$
腕の長さは0だということが分かりました。わざわざ計算しなくても、図を見れば力\(F\)のベクトルを延長すると回転中心\(O\)を通るので距離が0であることはすぐにわかります。
腕の長さが0であるということはモーメントも0であるということになります。このことから、半径方向に働く力のモーメントは0であるということが言えます。
腕の長さの深掘り別解
「半径方向の力のモーメントは0」ということを理解すると、一つ前の例で別解が考えられるようになります。
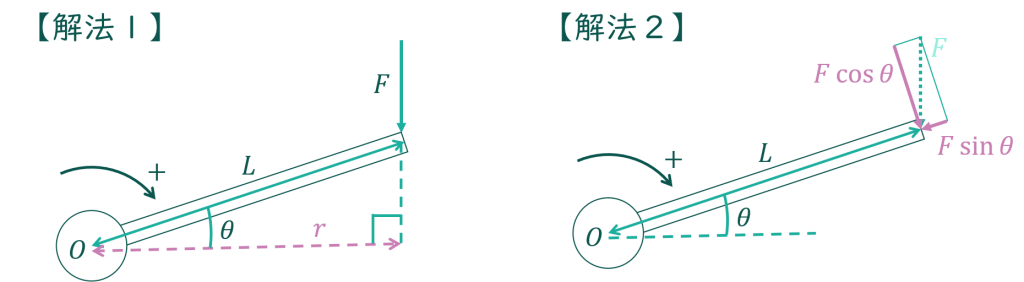
力\(F\)を半径方向の力\(F\sin\theta\)と回転方向の力\(F\cos\theta\)に分解します。半径方向というのは回転中心を通る方向で、回転方向というのは半径方向と垂直に交わる方向です。分解の方法は斜面の物体に働く重力の分解と同じです。
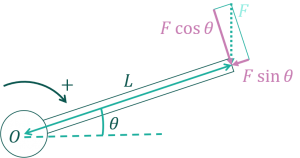
力の分解がわからない方はこちら
\(F\sin\theta\)は半径方向の力になっているので、モーメントは0になります。なので、もう一つの力である\(F\cos\theta\)についてだけ考えればよいです。
力 \(F\cos\theta\) の腕の長さは\(L\)です。したがって、モーメントは次式となります。
$$M=LF\cos\theta$$
最初に説明した解き方と同じ答えになっていることが分かります。つまり、力のモーメントを求めるときは
①回転中心から力までの最短距離を求めて腕の長さとする
②力を分解して回転方向のみを考える
という2つの考え方ができます。どちらでも結果は同じなので、問題に応じて計算が簡単そうな方を選びます。
力が複数の場合
次は力の数を増やしてみます。
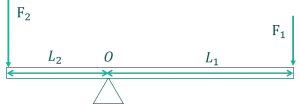
棒の両端にそれぞれ力\(F_1,F_2\)が働いていて、その間に支点\(O\)があります。支点\(O\)から力\(F_1,F_2\)までの距離(腕の長さ)はそれぞれ\(L_1,L_2\)です。力は釣り合って静止しているものとします。
静止しているということは、2つの力のモーメントが釣り合っているということを意味しています。運動方程式と同じようにモーメントでもつり合いの式を立てることができます。
棒に加わる力のモーメントをそれぞれ求め、つり合い式を立てます。
$$L_1F_1\cos\theta-L_2F_2\cos\theta=0$$
\(F_1\)は棒を時計回りに回そうとする力なので正の値とし、\(F_2\)は棒を反時計回に回そうとする力なので負の値としています。
右辺が0なのは運動方程式と同様に、力のモーメントが釣り合っており、棒は動き出さないということを示しています。運動方程式と異なり、高校レベルの力学では右辺は常に0になります。
運動方程式がわからない方はこちらをどうぞ
力が釣りあっていない回転運動を考える場合は右辺にも式が必要ですが、これには大学の主に機械工学科で学ぶ慣性モーメントという概念が必要になり、一気に難易度が上がります。機会があれば紹介します。
回転中心の位置
これまで直感的にわかりやすいように、回転中心を探し、その点回まわりのモーメントを考えてきました。しかし、モーメントを考える点は必ずしも回転中心である必要はありません。どこでも好きな点を選んで、その点まわりのモーメントを考えてよいです。
試しに先ほどの例で、別の点のまわりのモーメントを考えてみましょう。試しに力\(F_2\) が作用している点を\(O’\)と定義し、点\(O’\)まわりのモーメントを考えてみましょう。
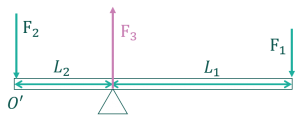
実は先ほどの例では出てきませんでしたが、\(F_3\)という力が支点に働いています。なぜ先ほどの例では無視していたかというと、支点まわりのモーメントを考えていたため、支点に働く力は腕の長さが0となっていたからです。その結果モーメントも0になるため、わざわざ考える必要がありませんでした。
しかし今回はモーメントを考える点が\(O\)から \(O’\) にずれたため、力\(F_3\)も計算に加える必要があります。なので、まずは 力\(F_3\) を求めます。
力\(F_3\) は上下方向の力のつり合いから求められます。
$$F_3-F_1-F_2=0 \\ \leftrightarrow F_3=F_1+F_2$$
点\(O’\)まわりのモーメントのつり合い式を立て、上で求めた\(F_3\)の値を代入して計算していきます。
$$(L_1+L_2)F_1-L_2F_3=0 \\ \leftrightarrow (L_1+L_2)F_1-L_2(F_1+F_2)=0 \\ \leftrightarrow L_1F_1+L_2F_1-L_2F_1-L_2F_2=0 \\ \leftrightarrow L_1F_1-L_2F_2=0$$
先ほど求めたの点 \(O\) まわりのモーメントの式と一致することが分かります。
このように、モーメントを考える点はどこを選んでも問題ありません。ただし、 点\(O’\)まわりのモーメントを求めたときの力\(F_3\)のように、追加で運動方程式を立てる必要が出てくる場合もあります。感覚的には未知数となっている力が働いている点を選択するとうまくいく場合が多いと思います。
長くなりましたが、これでモーメントの説明は以上です。
身に着けたいセンス
最後に身に着けて起きたいモーメントのセンスを説明します。先ほどの例で求めたモーメントのつり合い式を変形していきます。
$$L_1F_1-L_2F_2=0 \\ \leftrightarrow F_1=\frac{L_2}{L_1}F_2$$
ここで、\(L_1\)は\(L_2\)の二倍の長さだとします。上の式に\(L_1=2L_2\)を代入します。
$$ F_1=\frac{L_2}{2L_2}F_2 \\ \leftrightarrow F_1=\frac{1}{2}F_2$$
この式が意味ていているのは、力\(F_1\)は力\(F_2\)の半分の大きさでつりあうということです。例として棒の左端に10kgの物体が乗っていた場合を考えます。この場合、右端に5kg以上の力を加えれば物体を持ち上げることができるということになります。
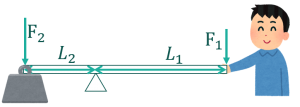
ここまでは単純なてこの原理なので理解できていると思います。ポイントはここからです。この時、棒の両端の移動量はどんな関係があるでしょうか?
右端を押し込んで棒を\(\theta\)回転させたとします。このときの棒両端の軌跡(通り道)を考えてみましょう。

軌跡は扇型の弧になります。初めて出てくる公式ですが、弧の長さは\(L=r\theta\)で求めることができます。ただし、\(r\)は半径、\(\theta\)は弧度法で表した中心角です。
この式を使うと、両端の移動量\(a,b\)はそれぞれ次式となります。
$$a=L_1\theta=2L_2\theta \\ b=L_2\theta$$
この式からaの移動量はbの2倍になっているとが分かります。
整理すると、必要な力が半分になる代わりに動かす量は倍になると言うことになります。少し抽象化すると、「必要な力が1/nになると移動量はn倍になる」と言えます。
この「軽い力で動かす場合はいっぱい動かす必要がある」あるいは 「いっぱい動かす必要がある場合は軽い力で動かせる」 という感覚は様々なところで活きるのでぜひ身につけておいてください。具体的には、滑車の設計、ギアの設計、油圧の設計などで必要になります。
まとめ
今回は力のモーメントの説明をしました。ポイントをおさらいしておきましょう。
- モーメントは腕の長さと力大きさの積で表される
- 時計回りを正、反時計回りを負とする
- 腕の長さは、注目している点から力のベクトルまでの距離
- 半径方向に働く力は腕の長さが0なのでモーメントも0
- 必要な力が1/nになると移動量はn倍になる
-
前の記事
摩擦係数の測り方|初心者のための力学入門 2021.05.31
-
次の記事
仕事とエネルギー | 初心者のための力学入門 2021.06.19