力の合成と分解 | 初心者のための力学入門
力学のあちこちで登場する力の合成と分解について説明します。簡単に言ってしまうとベクトルの計算です。これを理解するためには 高校1年レベルの三角比の知識が必要になるので先に説明します。数学Bでベクトルを履修済みの方は「力の分解」の項目から読んでください。
力が分からない方は先にこちらをご覧ください
三角比
三角比とはsin(サイン)、cos(コサイン)、tan(タンジェント)で表される直角三角形の辺の長さの比のことです。下図のような角度θ(シータ)と角度90°の角を持つ直角三角形を考えます。
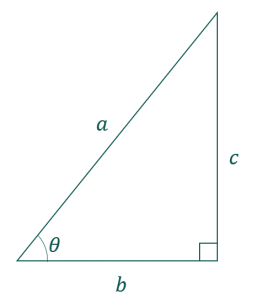
sinθ、cosθ、tanθはそれぞれ辺の長さを使って、
$$\sin\theta = \frac{a}{b}$$ $$\cos\theta = \frac{a}{c}$$ $$\tan\theta = \frac{b}{c}$$
と表せます。大事なのはどの辺が分母で、どの辺が分子になっているかです。これは確実に覚えてください。sin,cos,tanの頭文字を使った覚え方が有名です。
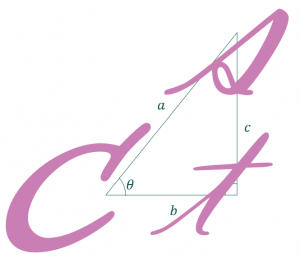
筆記体でs,c,t を書くときに通るところが分母と分子になっています。
三角比の値は角度θのみで決まります。辺の長さは関係ありません。θが同じなら三角形は相似だからです。
三角比の値はExcelやgoogleスプレッドシートなどの表計算ソフトで簡単に計算できます。今回は試しにsin30°を計算してみます。
普段よく目にする直角を90°とする角度の表し方は「度数法」と言います。実は 度数法は 数学や物理の世界では一般的ではありません。より一般的なのは直角を\(\pi/2\)radとする「弧度法」です。radの読み方はラジアンで、弧度法で角度を表す時の単位です。
表計算ソフトも例外ではなく、三角比を扱うときは弧度法を使用しなければなりません。なのでsin30°を求める場合、「度数法を弧度法に変換する」→「三角比を計算する」の2段階の計算が必要になります。
それではExcelを使って確認しましょう。三角比を求めたい角度を度数法でB1セルに入力します。

度数法を弧度法に変換するときはRADIANS関数を使用して、=RADIANS(B1)のように入力します。この式をB2セルに入力してください。

最後に三角比を求めます。SIN関数、COS関数、TAN関数を使用します。わかりやすいですね。=SIN(B2),=COS(B2),=TAN(B2)をそれぞれB3,B4,B5セルに入力してみてください。
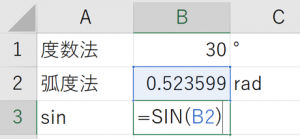
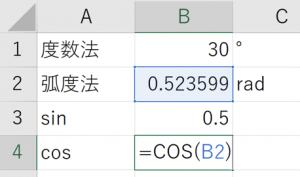
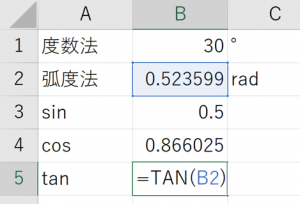
値を見ても正しいのかよくわからないと思いますが、おそらく問題ありません。今回はわかりやすくするために複数行に分けて書きましたが、実際は”=SIN(RADIANS(30))”のように一つのセルで一気に計算してしまうことも多いです。
ここまでが分かればひとまず三角比はOKです。
力の合成(ベクトルの和)
力はベクトルで表されます。ベクトルであるというのは、向きと大きさを持つということです。一般的に矢印の向きと長さでベクトルの向きと大きさを表します。
例えば童話の「おおきなかぶ」を考えてみます。この話では地面に埋まったかぶを引き抜くためにみんなで力を合わせます。

みんなは同じ方向に同じくらいの大きさの力を加えています。同じ向きだからこそ大きな力となってかぶがぬけるのです。
今度は綱引を考えてみます。綱引きは2つのチームが反対方向に力を加えます。
力の向きが反対の場合、力が打ち消しあって綱があまり動かないのがわかると思います。
このように複数の力が加わる場合、大きさが同じであっても向きが異なると結果が大きく変わります。
「力を合わせる」「打ち消しあう」などと言いましたが、複数の力を合算するにはどうしたらよいか考えていきます。
結論から言うと「図でベクトルをつなげる」ということになります。例えば下向きに働く力と右向きに働く力があったとします。

まず、どちらかのベクトルの終点ともう一方のベクトルの始点をつなげます。

1つ目のベクトルの始点と、2つ目のベクトルの終点をつなぐベクトルを新たに書きます。(下図紫色)

これだけです。この紫色のベクトルこそが、二つの力を合成した新しい力となります。「下方向と右方向の二つの力が加わっている」というのと「合成した力のみがかかっている」というのは全く同じ状態を表します。
当然ながら、合成後の力を使って計算したり動きを考えたりする場合は、もともとの二つの力は無視しなければならいことに注意してください。合成はあくまで「置き換え」のための手法です。
力を一つにまとめることで、物体が動こうとする向きがわかったり、計算が簡単になったりするメリットがあります。
今回は2つの力で考えましたが、3つ以上の力でも同じように合成できます。順々に終点と始点をつないでいき、一番最初の始点と一番最後の終点を結ぶベクトルを書けばそれが合成した力にになります。
力の分解
力の分解は、前項で説明した力の合成の逆です。つまり、一つのベクトルを複数のベクトルに分けるということです。次のベクトルを2つのベクトルに分けてみましょう。
まず、ベクトルの始点を通るように二つの直線を書きます。この直線の向きが分解した力の向きになるので状況に応じて最適な向きを選定する必要があります。力学でベクトルの分解をするときは直角に交わる二直線を取ることが多いので、今回もそうします。
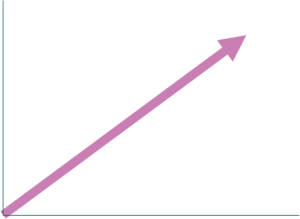
次に、分解したいベクトルが対角線となるような長方形を書きます。この時、先ほど追加2つの直線の上に辺が乗るようにします。
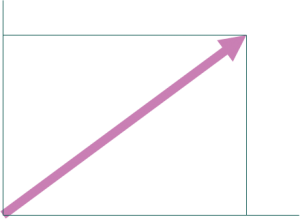
この長方形の2辺が分解されたベクトルとなっています。
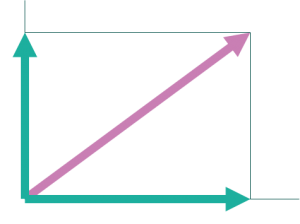
今回は直角に交わる二直線を選んだので長方形となりましたが、直角ではないに直線を使って分解することも可能です。その場合、長方形と説明したところが平行四辺形になります。例えばこんな感じです。
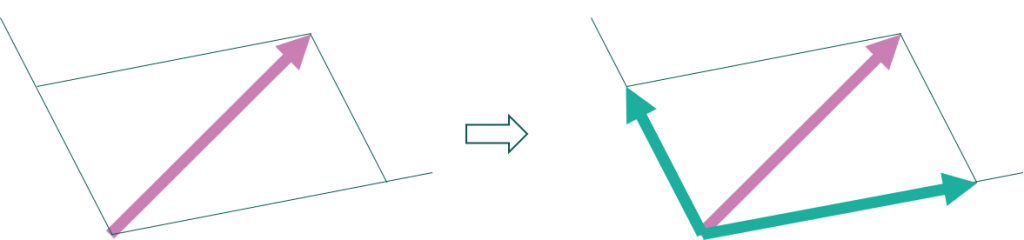
分解前のベクトルの大きさ(=力の大きさ)をFとしたとき、分解後の2つのベクトルの大きさはどうなるでしょうか?
ここで三角比が登場します。分解前のベクトルと分解後の右方向のベクトルがなす角をθとします。
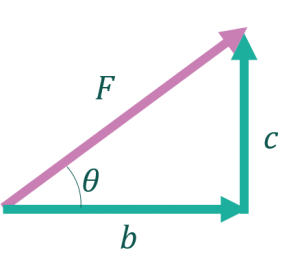
Fとθは計算の都合上文字になっているだけで、実際には具体的な値がわかっていいます(問題文で与えられていたり、自分が決めたり)。このことを「Fとθは既知」と言います。つまり、Fとθを使ってbとcを表すのがゴールです。
そのためにはsinとcosを使います。それぞれ公式に当てはめてみましょう。
$$\sin\theta = \frac{c}{F}$$ $$ \cos\theta = \frac{b}{F} $$
これを、bとcについて解きます。
$$c = F\sin\theta$$ $$ b = F\cos\theta $$
このようにして分解したベクトルの大きさを求めることができます。
よく見る力の分解
最後にまとめとして、力学で非常によく目にする問題を説明しておきます。それは「斜面にある物体」です。

物体には常に下向きに重力が掛かるため下向きの矢印が示されています。力の大きさはmgとします。斜面の角度θは既知です。
斜面の問題では斜面と平行な向きの力と、斜面と直行する向きの力に分解するのが定石です。分解後の力を追記するとこのようになります。
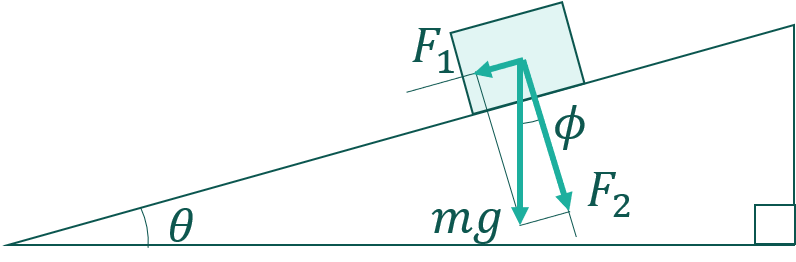
分解後の力(\(F_1,F_2\))の大きさを求めます。 力を分解する方向は勝手に決めたので \(\phi\) は未知数です。 \(\phi\)(ファイ)が分かれば \(F_1,F_2\) も求められそうですね。図を見ると直感的に\(\phi = \theta\)が成り立ちそうな気がします。実際その通りなので、図形の問題として解いてみます。
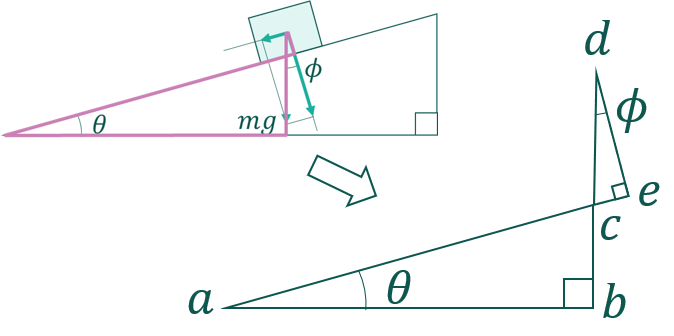
紫色の線分だけを取り出して二つの三角形(△abc、△dec)に着目します。対頂角の大きさは等しいので\(∠acb=∠dce\)が成り立ちます。また、 辺deは\は斜面と直角になるように引いた線なので (∠dec=90°\) です。したがって、\(∠abc=∠dec=90°\)となっています。
△abcと△dec は二つの角が等しいという相似条件を満たしています。相似な三角形は対応する角の大きさが同じになるので\(\theta = \phi\)が成り立ちます。
あとは三角比を使って\(F_1,F_2\)を求めるだけです。ただ、今の姿勢だとsinθ、cosθがどこの辺の比になるのかがわかりにくいかもしれません。分かりにくければ次のように変形してください。
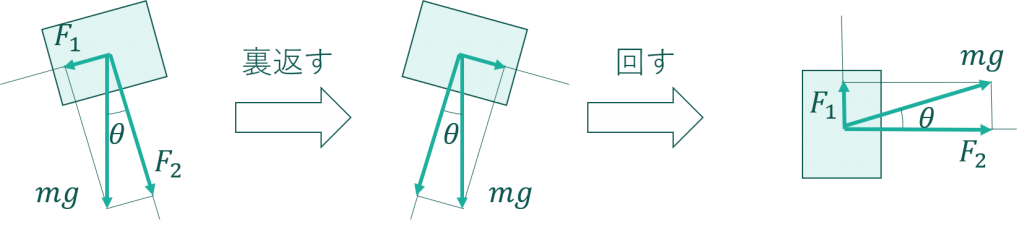
この姿勢にすれば三角比のセクションで説明したときと全く同じですね。したがって、
$$\sin\theta=\frac{F_1}{mg} \rightarrow F_1=mg\sin\theta$$ $$\cos\theta=\frac{F_2}{mg} \rightarrow F_2=mg\cos\theta$$
となります。元の姿勢に戻すと次のようになります。
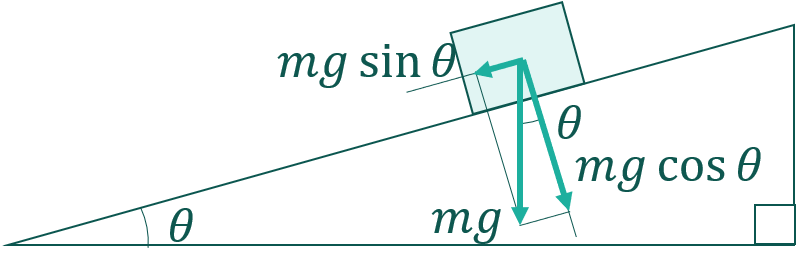
今回はこれで終わります。力の分解はすべての力学問題で出てくると言っても過言ではないくらい重要です。今回は説明のために三角形の姿勢を変えて三角比を考えやすいようにしましたが、わざわざ姿勢を変えなくても、どんな姿勢の三角形でもsin,cosを使って辺の長さを求められるようにしておいて下さい。
-
前の記事
記事がありません
-
次の記事

運動方程式 | 初心者のための力学入門 2021.05.14
