ギア設計の基礎知識 | 初心者の為の機械設計
今回は機械要素の中でも最も重要と言えるギア設計について2回に分けて説明します。今回はギアを設計する上で最低限身につけてときたい用語と基本的な特性を説明します。
ギアが設計できるようになると動くものを設計できるようになります。3Dプリンターを持っているのに動かないばかり作っている方などに非常に役立つ内容になっています。ぜひ最後までご覧ください。
ギアとは?
ギア(=歯車)は回転によって力を伝達する機械要素です。自転車、自動車、掃除機、プリンタなど身の回りの様々な工業製品で広く使用されています。
代表的なギアの種類には「平歯車」「はすば歯車」「ウオームギア」「ラック&ピニオン」「かさ歯車」などがあります。
中でも特によく使うのは平歯車とはすば歯車です。はすば歯車は設計が若干難しいので、今回は最もシンプルがなギアである平歯車を設計していきます。
ギア設計
ギア設計を端的に言うと、モーターやエンジンなどからギアへ入力される回転を、狙った回転数、トルクに変換することです。
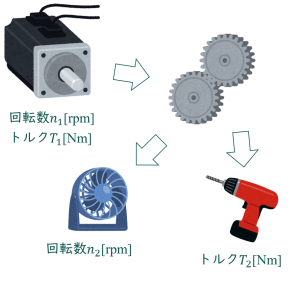
回転数というのは回転のスピードどのことです。1分間で何回転するかで表すことが多く、rpmという単位で表します。多くの車のメーターにエンジンの回転数が表示されているのでご存じの方も多いと思います。
トルクという言葉も一度は耳にしたことがると思います。おそらく回転の力強さのようなイメージを持っているかと思います。そのイメージで正しいです。これまでに説明してきた言葉で言うと「力のモーメント」のことです。 トルクと力のモーメントは基本的に全く同じものだと理解していただいて良いです。しいて言えば、ギアやネジのような、明確な回転軸がある場合にトルクという言葉を使うことが多いように思います。
力のモーメントがわからない方はこちらをどうぞ
なぜ回転数やトルクを変える必要があるかというと、モーターやエンジンのような動力は一般的に回転数が高く、トルクが低いためです。もちろんそのままの回転数・トルクで使用できる場合もありますが、多くの場合変換が必要です。
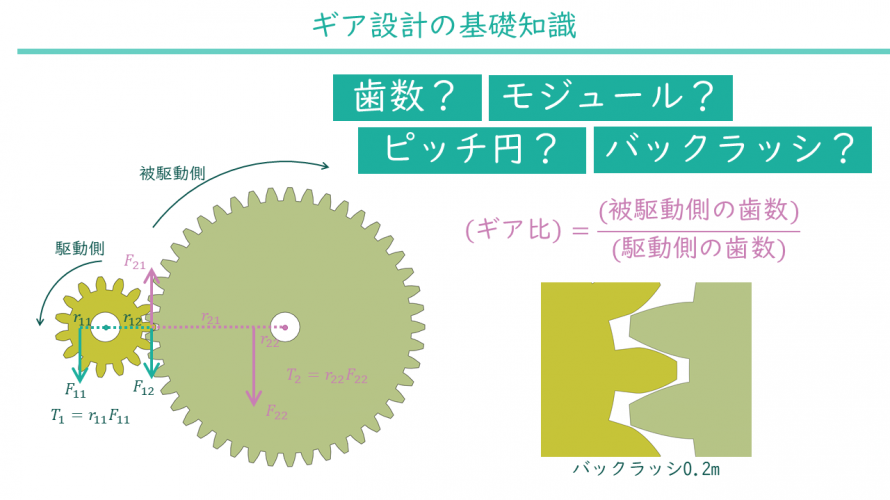
まずはモジュール、歯数、ピッチ円、バックラッシュの4つを適切に設計できるようになりましょう。最低限これだけ身に着ければそれなりに動くギアが作れます。
歯数
まずは歯数(はかず)から説明します。
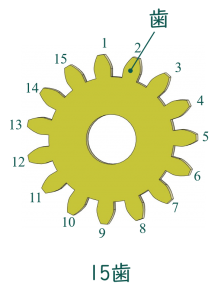
ギアは複数の突起が円周上に並んだ形をしています。この一つ一つの突起を歯と言います。この歯が全部で何個あるかが歯数です。歯数の単位はずばり”歯”で、1歯(いっぱ)、2歯(には)と数えます。
15歯のギアと45歯の用意しました。歯数が多いほうが大きいことが分かります。

早速ですが、2つのギアを連結して回してみます。
最初に15歯の方を一周回してみます。すると45歯の方は1/3周回ります。
逆に45歯の方を一周回すと15歯のギアは3周回ります。
このように歯数が異なるギアをくみあわせることで、回転数を変化させることができます。また、ギアによってどれだけ速度が変わるかは歯数によって決まります。
変速の割合を表す言葉はたくさんあり、ギア比・減速比・変速比・速度伝達比などがあります。業界や状況に応じて使う言葉が変わったり、名前は違っていても同じものを指していたりします。ここでは噛み合う2つのギアでどれだけ減速するかをギア比と呼び、3つ以上のギアを連結させて多段階の減速を行ったときに入力と出力でどれだけ減速したかを減速比と呼ぶことにします。
ギア比は次の式で求められます。
$$(ギア比)=\frac{(被駆動側の歯数)}{(駆動側の歯数)}$$
駆動側というのは回す方のギアのことで、被駆動側というのは回される方のギアのことです。ギア比が大きくなればなるほど、大きな減速効果を得られます。
ギア比は「3:1」のような書き方をします。ギア比が小数になった場合でも「3.2:1」のように「:1」の部分は変わりません。「:」は「/」と読み替えて分数のイメージを持ってもらうのが良いと思います。ギア比以外では設計図を製図する際の縮尺でも同じ表記が使用されており、10分の1のことを1:10と書きます。
ギアによって回転数が変わるのと同時にトルクも変わります。
力のモーメントで説明した”センス”で考えると、「ギア比が大きい→減速が大きい→たくさんギア回しても相手のギアがあまり回らない→軽い力で動かせる」という論理で考えることができます。
次の図を使ってモーメントの釣り合い式立てて考えてみましょう。
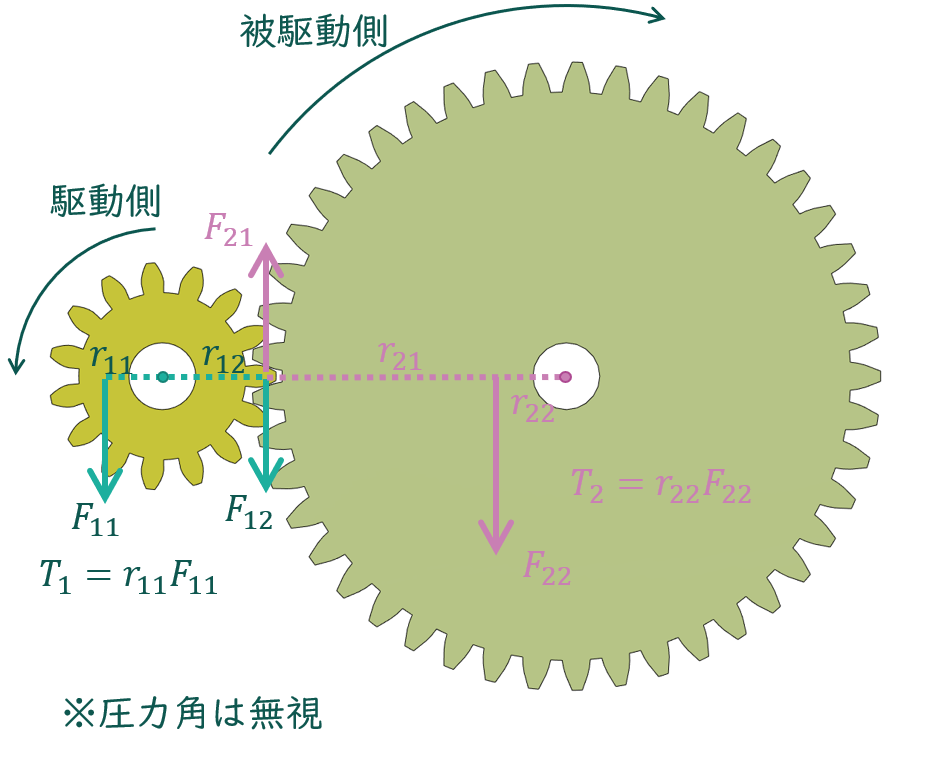
駆動側ギアの半径\(r_{11}\)の所に入力として力\(F_{11}\)を作用させると想定します。この力によるトルク \(T_1\)は力のモーメントの式から \(T_1=r_{11}F_{11}\)となります。 ギア同士が接触している点では、駆動側ギア、被駆動側ギア両方に同じ大きさの力 \(F_{12},F_{21}\)が働きます(作用反作用の法則)。被駆動側ギアの半径 \(r_{22}\)の所から出力として力 \(F_{22}\)を取り出します。この力をトルクで表すと \(T_2=r_{22}F_{22}\)となります。
駆動側のモーメントのつり合い式を立てると次のようになります。
$$r_{12}F_{12}-T_1=0 \cdots (1)$$
作用反作用の法則から次の式が成り立ちます
$$F_{12}=F_{21} \cdots(2)$$
被駆動側ギアのモーメントのつり合い式は次のようになります。
$$r_{21}F_{21}-T_2=0 \cdots(3)$$
これで必要な式は出そろったので、(1)~(3)を連立方程式として解きます。すると次の式が得られます。
$$T_2=\frac{r_{21}}{r_{12}}T_1$$
この式からわかるのは入力トルク \(T_1\)の \(r_{21}/r_{12}\)倍のトルク \(T_2\)が出力されるということです。
詳細は後述しますが、 \(r_{21}/r_{12}\) はギア比と一致します。
つまりギア比が3:1の場合、回転数は1/3、トルクは3倍になるということです。実際には摩擦によるロスなどの影響を受けてトルクは3倍より若干小さい値になります。詳細は次回説明します。
ギアによって減速した回転は、別のギアを用いてさらに減速させることも可能です。
被駆動側と呼んでいたギアに歯数が異なるギアを接続し、これを新たな駆動側ギアとして二段目の減速ををしてみます。図にすると次のようになります。
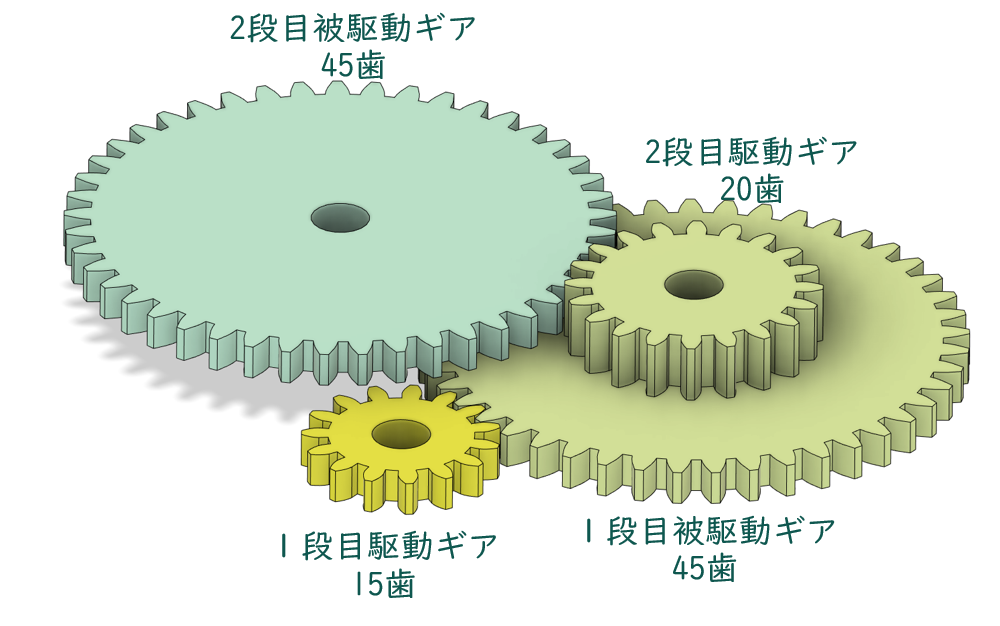
このギア列の真ん中で使用されているような、歯数が異なる複数のギアが一体となっているギアを段付きギアと言います。
これまで説明してきた通り 、一段目のギア比は3:1となっています。
二段目は駆動側ギアの歯数が20歯、被駆動側ギアの歯数が45歯となっているので、ギア比は2.25:1となっています。
二段減速のとき、格段のギア比かけると全体での減速比を求めることができます。したがって、この二段減速機の減速比は6.75:1ということになります。
このように歯数を決めるだけで回転数とトルクを自由自在に決められるようになります。
モジュール
モジュールはギアの歯の大きさを表す指標です。モジュール1のギアとモジュール2のギアを比較するとこのようになります。歯数はどちらも15です。

モジュールが大きいギアのほうが歯が大きくなっており、モジュールが違うと歯が噛み合わなくなってしまいます。
また、同じ歯数の場合はモジュールが大きい方がギアの円が大きくなることも分かります。
大きいモジュール、小さいモジュールにはそれぞれメリット・デメリットがあります。例えばモジュールを小さくすれば小型化できるというメリットがありますが、歯の強度が下がるというデメリットもあります。ギア設計ではこの辺りのバランスを考えるのも重要です。最初のうちはサイズが許す限り大きいモジュールを使っておけばよいと思います。
モジュールと歯数を決めればギアの大きさ、回転数、トルクが決まります。ここまでで設計の8割くらいはできるようになっていると思います。あとはギアをどのように配置するかを決めれば完了です。
ピッチ円
ピッチ円とはギアの中心からギア同士が接触する点までの距離を半径とする円のことです。モーメントのつり合い式を考えたときに2つのギアの歯が接触するする点を定義してぞれぞれのギアの半径\(r_{12}\)及び\(r_{21}\)を決めました。この半径をピッチ円半径と呼び、ピッチ円半径から描かれる円をピッチ円と呼びます。
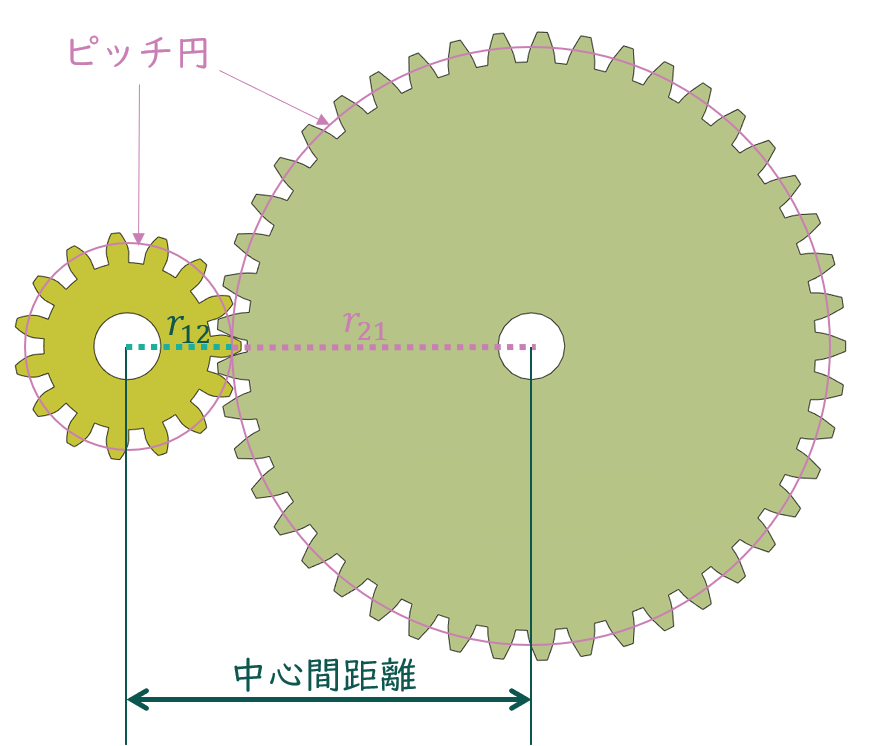
厳密に言うと、ギアの回転に伴って歯同士が接触する点は変化するので、上の説明は正しくありません。ただ、この説明が一番イメージしやすいと思うので、まずはこの認識で良いと思います。
ピッチ円の直径\(d\)はモジュール\(m\)と歯数\(z\)を用いて次の式で表せます。
$$d=mz$$
ピッチ円半径 \(r\)は直径の半分なので次式となります。
$$r=\frac{d}{2}=\frac{mz}{2}$$
これは歯数の項目で説明した\(r_{12}\)及び \(r_{21}\)に相当します。つまり次の式が成り立ちます。
$$\frac{r_{21}}{r_{12}}=\frac{ mz_2/2 }{mz_1/2}=\frac{z_2}{z_1}$$
というわけでここで改めて \(r_{21}/ r_{12} \)がギア比と一致するということが示されました。
二つのギアの中心間距離 \(a\) はそれぞれのピッチ円半径の和で表せます。片方のギアの歯数を \(z_1\)、もう片方のギアの歯数を \(z_2\)とすると、
$$a= \frac{mz_1}{2}+ \frac{mz_2}{2}= \frac{m(z_1+z_2)}{2}$$
と表せます。
基本的にはギア同士の中心間距離がこの距離になるように配置すればギアは正しく係合し、回転を伝達することができます。
バックラッシ
前項で求めた中心間距離には一つ問題があります。
それは隙間が全くないことです。計算通りにギアを配置し、係合部を拡大してみてみると次の図のようになっています。

2つの歯は隙間なく接触していることが分かります。一見すると、隙間がないのは良いことのようにも思えます。何が問題かというと、大きさのばらつきを吸収できないということです。
設計上の寸法と実際に製造した部品の寸法というのは全く同じになることはありません。実際の寸法は大きくなったり、小さくなったりします。
隙間がないような設計の場合、 大きめの寸法で出来上がった時にギアが噛み合うことができなくなってしまいます。
この問題を解決するために意図的に設けられた隙間のことをバックラッシと言います。
バックラッシの作り方には次の2種類があります。
- ギアの歯を小さめにする
- 中心間距離を広げる
今回は二番目の方法を紹介します。
方法は簡単で、前項で求めた中心間距離距離を若干大きめにしてギアを配置するだけです。問題は”若干大きめ”をどのように決めるかです。
場合によってどうするべきかは変わりますが、モジュールの0%~25%くらいにするのが一般的かと思います。つまり、モジュールが1の場合0~0.25mm中心間距離を大きめにします。
0.2m(mはモジュールの値)だけ中心間距離を広げてみると次のようになります。

設計上は少し隙間ができたので、ギアが干渉することはなさそうです。
私が使用している3Dプリンターは若干大きめにできる癖があるので、まずはモジュールの20%くらい中心間距離を広めにして設計しています。現物を確認して、隙間が詰められそうであれば15%などに詰めたりしています。
モデリングの方法などは近々fusion360の記事で紹介する予定なのでしばらくお待ちください。
まとめ
今回はギアの役割を説明したうえで、ギアを設計する必ず理解しておくべき「歯数」「モジュール」「ピッチ円」「バックラッシ」について説明しました。
これらを理解できれば狙った回転数、トルクになるようなギア構成を考え、適切に配置することができるようになります。
より具体的な設計手順については次回紹介します。
-
前の記事
摩擦係数の測り方|初心者のための力学入門 2021.05.31
-
次の記事
ギア設計の実践 | 初心者のための機械設計入門 2021.06.24