運動方程式 | 初心者のための力学入門

力学の中で一番重要である運動方程式を説明します。初めて力学を学ぶ方でもわかるように、四則演算以外の背景知識はなくても理解できるようにしています。
運動方程式
運動方程式は「力(F)は質量(m)と加速度(a)を掛けたものである」ということを表した方程式です。
$$F=ma$$
質量は体重などで馴染み深いkg単位で表される重さの値です。加速度は1秒間にどれだけ速度が変化するかを表す値です。加速度は馴染みがないと思うので詳しく説明します。
加速度
自転車を例に説明します。自転車はペダルを漕ぐと加速し、ブレーキをかけると減速する乗り物です。これを速度 [m/s(メートル毎秒)]と時間[s(秒)]のグラフで表してみます。
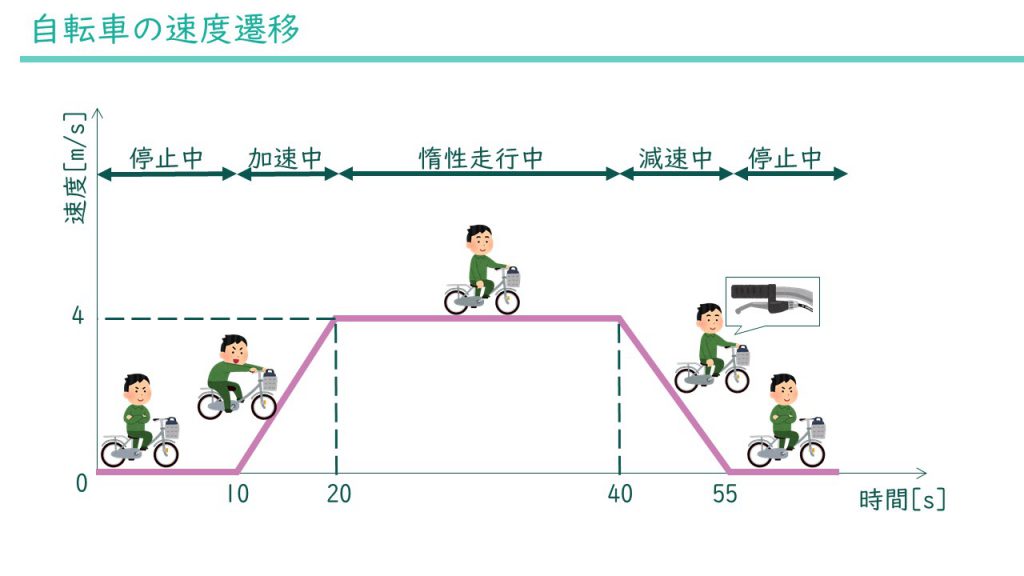
一番最初のまだ漕ぎ始めていない段階では速度が0です。ペダルを漕ぐと徐々に速度が上がります。ある程度早くなると、ペダルを漕ぐのをやめてもほんとんど減速せずに走り続けます。最後にブレーキをかけると速度が下がり最終的に0になります。
ポイントは2つあり、一つは速度が変わるときは傾きが一定ということです。これは加減速時はそれぞれ1秒間に変化する速度が一定だと言うことを表しています。上のグラフの加速時で言うと、10秒から20秒の10秒間で速度が0m/sから4m/sに増加しているので、1秒間毎に速度が0.4m/sずつ増えていることがわかります。この一秒間に変化する速度を加速度と言い、単位\(\mathrm{m/s^2}\)(メートル毎秒毎秒)で表します。加速度は、速度と時間のグラフの傾きでもあります。また、加速度が一定となる動きを等加速度運動と言います。
少しだけ単位の話をしておきます。単位というのはその値がどのような計算で求められたかを表しています。これまでなんの断りもなく速度の単位としてm/sと言う単位を使用してきましたが、これは距離mを時間sで割って求めるということを示しています。さらに噛み砕いて言うと1sで何m位置が変わるかを意味しているとも言えます。
加速度は1mに何m/s速度が変化するかを示すと言いました。言い換えると、速度m/sを秒sで割って求めました。なので単位は\(\mathrm{m/s^2}\)となります。考え方は速度と同じです。比較すると次のようになります

もう一つのポイントは、力を加えない限り速度は一定だということです。自転車の例ではペダルを漕いだりブレーキをかけたりすることで力を加えています。それ以外の部分では速度変化は無く、グラフは横線になっています。速度0m/sで停止しているときは停止したまま、加速後にペダルを漕ぐのをやめたら速度4m/sを維持します。これは慣性の法則と言う重要な法則です。運動方程式は完成の法則が成り立つことを前提としています。
今度は物が落ちる場合を考えてみましょう。手に持っている物体を離すと重力によって物体は落ちます。その時の速度はどのようになっているでしょうか?グラフにするとこんな感じになります。
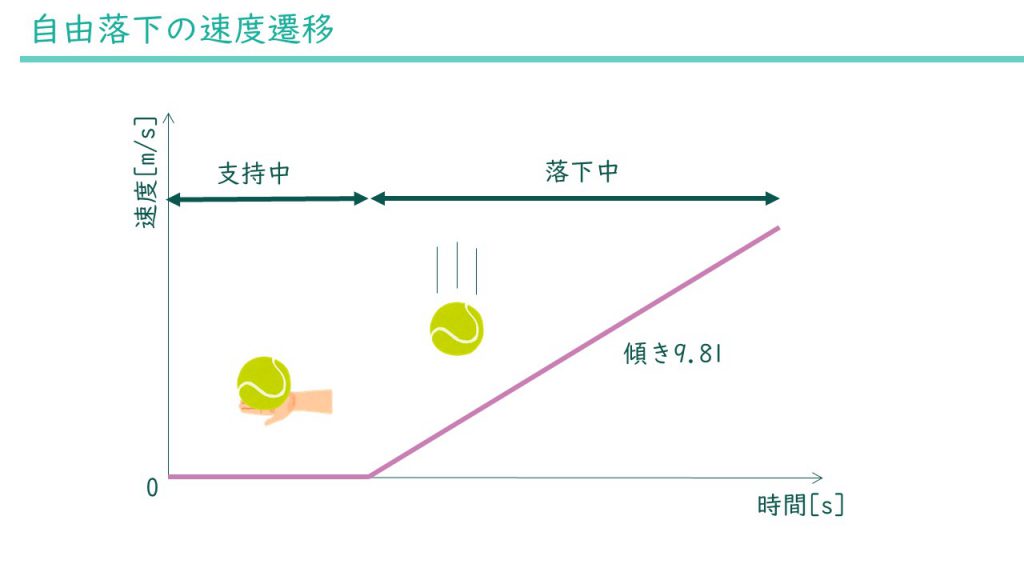
自転車のペダルを漕いだときと同じで一定の加速度で速度が増えていきます。この加速度は落下するものによらず9.81\(\mathrm{m/s^2}\)程度の値になります。この加速度を特に重力加速度と呼んでいます。重力加速度はgの文字で表します。
力
加速度の話はこれくらいにして、力の話をしましょう。冒頭で書いた通り、運動方程式は力、質量、加速度の関係を表した式でした。
$$F = ma$$
自転車の例に戻って考えてみましょう。ベダルを漕いで加速している時の加速度はすでに説明の通り0.4m/s2です。質量はまだ決めていなかったので50kgとしましょう。すると力は、\(F = ma = 50\mathrm{kg}\times0.4\mathrm{m/s^2} = 20\mathrm{kgm/s^2}\)と求められます。質量と加速度を掛けたので単位はkgm/s2となりますが、かなりの頻度で出てくる単位であるためこれを単にN(ニュートン)と置き換えます。
1Nは1kgの物体を1\(\mathrm{m/s^2}\)の加速度で移動させるために必要な力と言えます。今回の例では20Nの力が与えられることで、50kgの自転車と人が、加速度0.4\(\mathrm{m/s^2}\)で移動しているということになります。
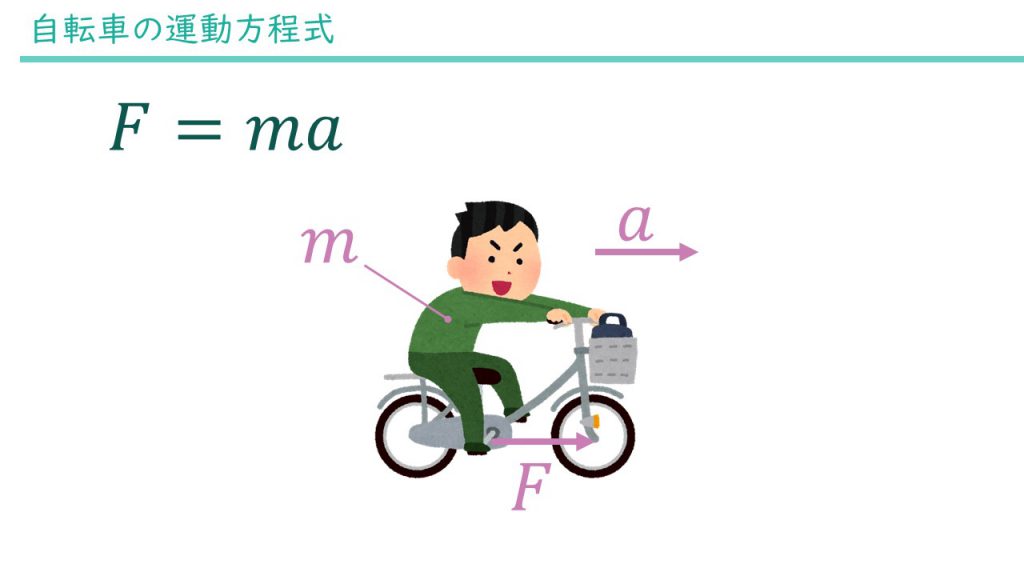
力は運転手がペダルに加えています。当たり前じゃないかと感じると思いますが、何がどこにどの向きで力を与えているかは力を考える上で一番と言っていいほど重要です。摩擦などが登場すると力の掛かり方を理解するのはかなり難しくなります(伏線)。
次に、もう一つの例だった物体の落下の方を考えてみましょう。ただ、落下しているときは自転車の場合と全く同じなので、物体から手を離す前を考えてみます。
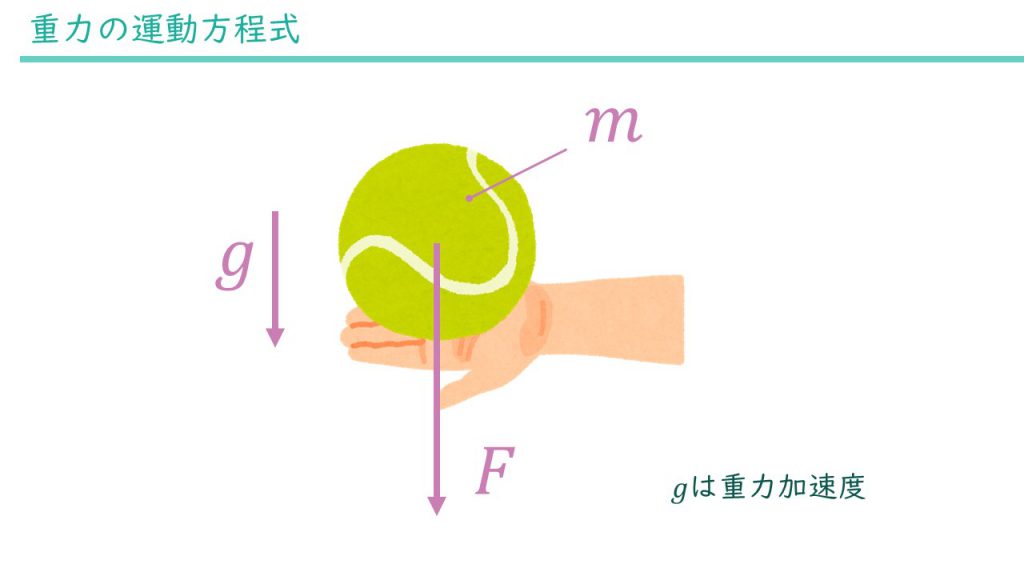
こちらも質量は決めていませんでした。球の質量は0.1kgとしましょう。重力加速度は常に下向きで一定の値なので、力は\(F = mg = 0.1\mathrm{kg}\times9.81\mathrm{m/s^2} = 0.981\mathrm{N}\)と求まります。
「力は物体がどんな加速度で移動するかを表す」と言ったのに、今回は動いていません。計算上は力が加わっていることになっているので矛盾します。これは一体どういうことでしょうか?
大抵の場合、加わる力は一つではなく色んな所に色んな向きで加わります。これを足したり引いたりして最終的に残った力によって動きが決まります。動きがない場合は、力が加わっていないか、力が釣り合っているかのどちらかです。今回は後者です。
基本的に2つの物体が接触しているところには何らかの力が働きます。逆は成り立たないので注意してください。例えば重力のように接触していなくても働く力もあります。さて、今回の場合、球と手が触れていますね。なのでここに力が働きます。球は手に支えられ、上方向に力を受けています。図で描くと次のようになります。
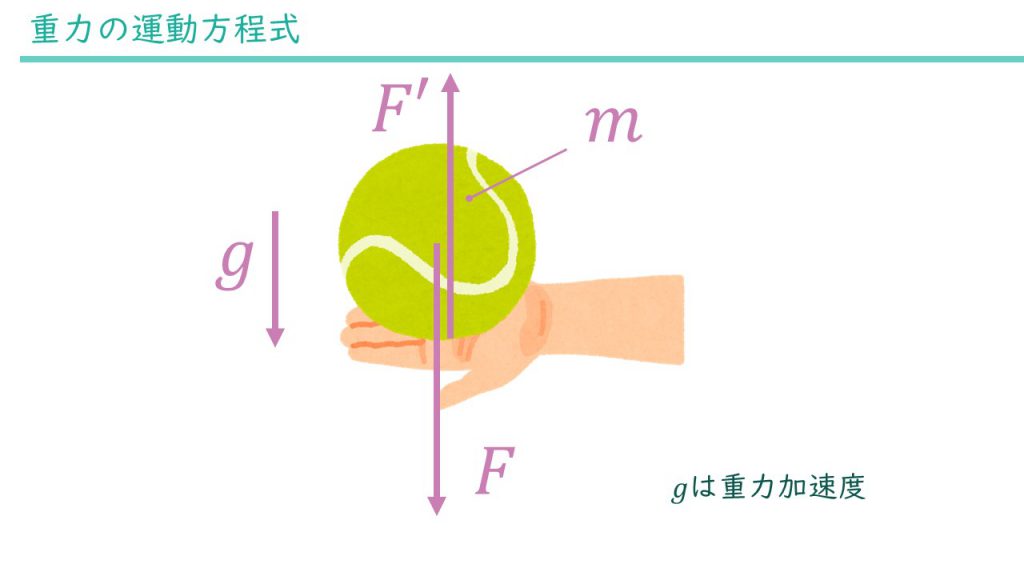
球が動いていないということは力は釣り合っているので、次の式が成り立ちます。
$$F’ -F = 0$$
式の基本は\(F=ma\)です。つまり、左辺に力を書き、右辺に質量×加速度を書きます。今回は球が動いていないので加速度は0となり、右辺が0になります。左辺は加わっている力それぞれの向きに気を付けて正負の符号をつけて合算します。今回は上方向に向く力を正とし、下方向に向く力を負としました。逆でも構いません。
この運動方程式は、手で支える力は球の重力に等しいので差が0であるという当たり前のことを表しています。
最後に力が釣り合わない場合を考えてみましょう。これまで説明したことを言い換えているだけですが、力が釣り合わないときは加速度を持って物体が移動します。球が上方向に移動すると考えるとこんな感じです。
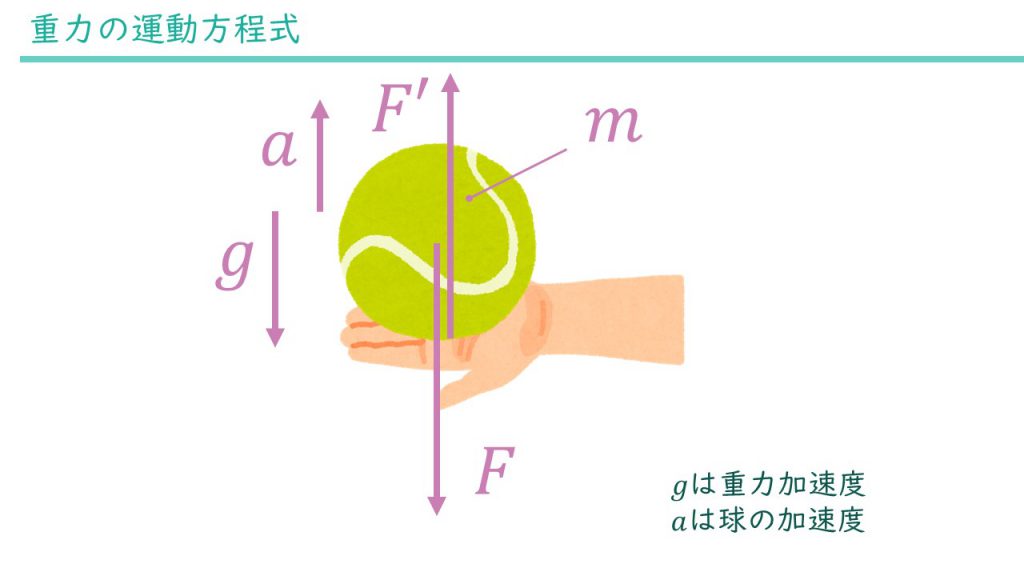
これをもとに運動方程式を建てると次のようになります。
$$F’-F = ma$$
静止時の運動方程式とは右辺が異なります。今回は力が釣り合っていないため球が動いています。そのため加速度が0にはならず、maが残ります。
この運動方程式は上方向の力F’と下方向の力Fの差で質量mの物体を加速度aで動かしているということを意味しています。
\(F=mg\)であることはすでに分かっているので、これを代入して
$$F’ – mg = ma\\
\leftrightarrow a=\frac{F’}{m}-g$$
このようにして加速度を求めることができます。手から加えられる力を2Nとすると加速度は
$$a=\frac{2}{0.1}-9.81=10.19[\mathrm{m/s^2}]$$
となります。このように、図を使って力の釣り合いを考え、力、質量、加速度のうちわかっているものをもとに、わからないものを求められるようになればひとまずOKです。
今回はここで終わりにして、次回摩擦を含む系の説明をします。
-
前の記事
力の合成と分解 | 初心者のための力学入門 2021.05.11
-
次の記事
摩擦力 | 初心者のための力学入門 2021.05.20